Nand2tetris - 从布尔逻辑到算数运算
本文是 nand2tetris 课程的读书笔记,不会列举过多细节,仅精炼出有意思的概念,供日后查阅。
从布尔逻辑的视角来看,所谓加法器只不过是一种特殊的逻辑结构。但是,我们 人类 为其加上的新的 解释,即【定长二进制加法】,因此它变得 有用。名字与实际结构,共同构成了事物的完整概念,从此,这种电路被称为加法器,不再有其它意义。
加法器的级联,使其扩充至 n-bit。
....
HalfAdder(a=a[0], b=b[0], sum=out[0], carry=carry1);
FullAdder(a=a[1], b=b[1], c=carry1, sum=out[1], carry=carry2);
FullAdder(a=a[2], b=b[2], c=carry2, sum=out[2], carry=carry3);
FullAdder(a=a[3], b=b[3], c=carry3, sum=out[3], carry=carry4);
FullAdder(a=a[4], b=b[4], c=carry4, sum=out[4], carry=carry5);
FullAdder(a=a[5], b=b[5], c=carry5, sum=out[5], carry=carry6);
FullAdder(a=a[6], b=b[6], c=carry6, sum=out[6], carry=carry7);
....
二进制补码,是用来表示有符号整数的工具。
依然是【名字】的作用,同样的操作序列,一旦我们将其重新解释,它立刻从无符号加法,变为有符号加法。
但这里有个技术问题,为什么二进制补码能够按照这样的方式工作?
在上大学的时候,老师直接告诉我们二进制补码的计算方式,即按位取反加1,并用时钟的工作方式,说明它的正确性。
在时钟上,正着走 3 步,等于反着走 12 - 3 步。
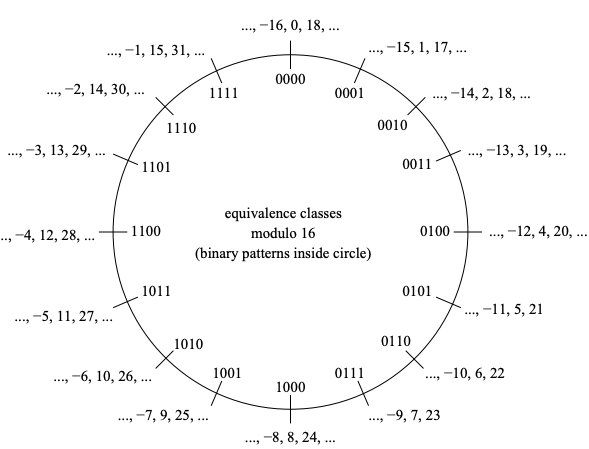
我们是否有办法证明补码的正确性呢?具体而言:
a + b 的补码,是否等于 a 的补码 二进制加 b 的补码
我把无符号二进制加法写作 \(+_2\),并将 a 的补码定义为 \(comp2(a)\)
我们将命题改写为:
\(comp2(a+b)=comp2(a)+_2comp2(b)\)
证明:
将原始无符号二进制表示为 \(bin(a)\),且要求 \(a \ge 0\),它具有以下性质:
- \(bin(a)=bin(a + k * 2^n)\),其中 \(k \gt 0\),这个很显然,因为是定长二进制,所以高位都丢弃了。
- \(bin(x+y)=bin(x)+_2bin(y)\),这条代表二进制加法的正确性,如果不成立,我们就别用这个工具了。
此外,补码的定义为:
\(comp2(a)=\begin{equation}
\begin{cases}
bin(a)& 2^{n-1} \gt a \ge 0\\
bin(2^n + a)& -(2^{n-1}) \le a \lt 0
\end{cases}
\end{equation}\)
于是,可以改写命题为:
\(bin(k*2^n+a+b)=bin(a+m*2^n) +_2 bin(b+l*2^n)\),其中 k,m,l 都非负。
使用上面的性质1,可以进一步改写命题为:
\(bin((k+k+m+l)*2^n+a+b)=bin(a+(m+k)*2^n) +_2 bin(b+(l+k)*2^n)\)
\(bin(a+(m+k)*2^n+b+(l+k)*2^n)=bin(a+(m+k)*2^n) +_2 bin(b+(l+k)*2^n)\)
令 \(x=a+(m+k)*2^n,y=b+(l+k)*2^n\),可以得到:
\(bin(x+y)=bin(x) +_2 bin(y)\),即上面的性质2,故原命题成立。
对于补码的理解,有一些资料可以参考:
https://en.wikipedia.org/wiki/Modular_arithmetic
https://igoro.com/archive/why-computers-represent-signed-integers-using-twos-complement/
https://courses.engr.illinois.edu/ece199/fa2012/notes/twos-complement.pdf
ALU
将一系列算术和逻辑运算打包到一个芯片里,并用控制位进行操作选择,就是 ALU。
CHIP ALU {
IN
x[16], y[16], // 16-bit inputs
zx, // zero the x input?
nx, // negate the x input?
zy, // zero the y input?
ny, // negate the y input?
f, // compute out = x + y (if 1) or x & y (if 0)
no; // negate the out output?
OUT
out[16], // 16-bit output
zr, // 1 if (out == 0), 0 otherwise
ng; // 1 if (out < 0), 0 otherwise
PARTS:
// x 的预处理
Mux16(a=x, b=false, sel=zx, out=zeroedX);
Not16(in=zeroedX, out=negateX);
Mux16(a=zeroedX, b=negateX, sel=nx, out=finalX);
// y 的预处理
Mux16(a=y, b=false, sel=zy, out=zeroedY);
Not16(in=zeroedY, out=negateY);
Mux16(a=zeroedY, b=negateY, sel=ny, out=finalY);
// 选择 and 或者 add
And16(a=finalX, b=finalY, out=andXY);
Add16(a=finalX, b=finalY, out=addXY);
Mux16(a=andXY, b=addXY, sel=f, out=computed);
Not16(in=computed, out=negatedComputed);
Mux16(a=computed, b=negatedComputed, sel=no, out[15]=signBit, out[0..7]=lowBit, out[8..14]=hiBit);
// 顺便输出状态位
And(a=signBit, b=true, out=ng);
And16(a[15]=signBit, a[8..14]=hiBit, a[0..7]=lowBit, b=true, out=out);
Or8Way(in=lowBit, out=notZeroLow);
Or8Way(in[0..6]=hiBit, in[7]=signBit, out=notZeroHi);
Or(a=notZeroLow, b=notZeroHi, out=notZero);
Not(in=notZero, out=zr);