WSABIE 算法解释

算法论文:WSABIE: Scaling Up To Large Vocabulary Image Annotation
介绍
WSABIE 是一个通用的打标签算法,无论对象是图像,视频,还是文本,只要能抽取出 feature,并提供一个固定的标签集合,就可以使用 WSABIE,由于算法的通用性,下文将需要打标签的东西称为 对象。
模型
1. Joint Word-Image Model
对于 WSABIE 来说,打标签的过程,就是计算所有标签与当前对象的相似性,并取出相似性最高的标签作为结果。由于对象的 feature 和标签是两种不同的东西,为了计算相似性,WSABIE 将它们映射到 同一个向量空间 \( R^D \) 。
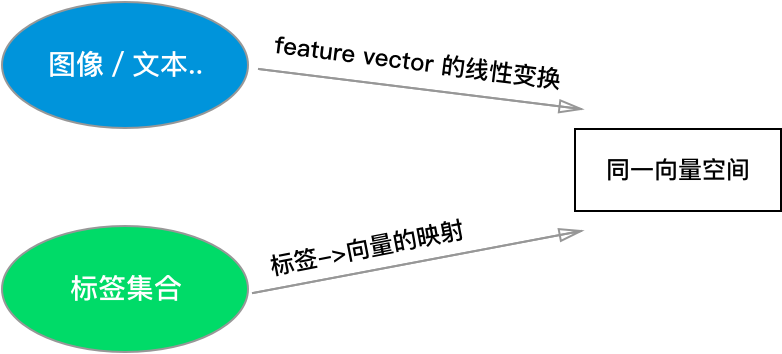
为了将对象 \(I\) 的 feature vector \( x \) 映射到 \( R^D \),只需做线性变换 \( \Phi _I(x)=Vx \),其中 \(V\) 是变换矩阵。
由于标签是离散的符号,为了将其映射到 \( R^D \),需要采用 Word2Vec 一样的思想,把它们转换成 embedding,换言之,我们把所有标签(假设有 \(N\) 个)对应的向量存在矩阵 \(W\) (大小 \(D \times N\))中,第 i 个标签就是矩阵的第 i 列: \( \Phi _W(i)=W_i \)
于是,对象 \( I \) 与第 i 个标签的相似度就是:
\[ f_i(x) = \Phi _W(i)^T \Phi _I(x)=W_i^TVx \]
模型中的待学习参数为线性变换矩阵 \(V\),以及所有标签的 embedding 向量 \(W\)。
2. 损失函数
每条训练数据都以 \( (x,y) \) 的形式存在,其中 \(x\) 是对象,\(y\) 是它唯一的一条正确的标签。
模型的优化目标,是让正确描述对象的标签,与对象有较高的相似度。更具体地说 \[ rank_y(f(x)) = \Sigma _{i \ne y} I(f_i(x) \ge f_y(x)) \]
这个式子表示 "排名大于 \(y\) 的标签的个数"(\(I\) 是示性函数),这条训练数据的误差是
\[ L(rank_y(f(x)))\]
其中
\[ L(k) = \Sigma _{j=1}^k \alpha_j \]
根据常数 \( \alpha_j \) 的取值的不同,我们可以得到不同的损失函数,所以 \( L \) 其实代表一类函数。
如果 \( \alpha_j \) 取值都为 \(C\), 那么如果 \(y\) 被模型排到第 \(k\) 名,损失值就是 \(Ck\)。论文中 \( \alpha_j = 1/j \)。
学习
WSABIE 对损失函数进行了一系列近似,让模型能够使用随机梯度下降(SGD)在线更新参数,这个学习算法是本文 最有价值的部分。下面依次介绍近似步骤:
1. 改写损失函数
\[ err(f(x), y) = L(rank_y(f(x)) \frac{rank_y(f(x))}{rank_y(f(x)) }\]
\[ =L(rank_y(f(x)) \frac{\Sigma_{i\ne y}I(f_i(x) \ge f_y(x))}{rank_y(f(x)} \]
\[ =\Sigma_{i \ne y} L(rank_y(f(x)) \frac{ I(f_i(x) \ge f_y(x))}{rank_y(f(x)} \]
2. 近似损失函数
使用 hinge loss 近似 0/1 损失函数,得到如下的近似损失:
\[ \overline{err}(f(x), y)=\Sigma_{i \ne y} L(rank_y^1(f(x)) \frac{ |1-f_y(x)+f_i(x)|_+}{rank_y^1(f(x))} \]
其中:
\[
rank_y^1(f(x))=\Sigma_{i\ne y}I(1+f_i(x) \ge f_y(x))
\]
使用这个近似的损失函数,得到在当前数据集分布的期望误差:
\[Risk(f)=\int\overline{err}(f(x), y)dP(x,y)\]
按照分布 \(P(x,y)\) 随机选择一个样本 \((x,y)\),计算其 \(\overline{err}(f(x), y)\),可以对这个期望误差进行估计。
实际上
\[ \Sigma_{i\ne y}\frac{ |1-f_y(x)+f_i(x)|_+}{rank_y^1(f(x))} \]
这个值,也可以通过采样进行估计,方法为,从满足 \( 1-f_y(x)+f_i(x) > 0 \) 的所有标签中,随机采样一个 \(\overline{y}\),计算 \( 1-f_y(x)+f_{\overline{y}}(x) \)
综上,总共两步采样:
- 随机选一个 \((x,y)\)
- 随机选一个标签 \( \overline{y} \)
得到 \(Risk(f)\) 的一个估计:
\[ \overline{err}(f(x),y,\overline{y})=L(rank_y^1(f(x))(1-f_y(x)+f_{\overline{y}}(x))\]
3. 随机梯度下降
接下来,就应用标准的随机梯度下降法,通过对 \(Risk(f)\) 的估计 \(\overline{err}(f(x),y,\overline{y})\) 求梯度,优化损失函数:
\[ \beta_{t+1}=\beta{t}-\gamma_t \frac {\partial\overline{err}(f(x),y,\overline{y})} {\partial\beta_{t}}\]
其中 \(\beta\) 是模型参数,也就是 \(W\) 和 \(V\) 矩阵。
4. 进一步优化性能
此时,每一步优化的性能还是不好,原因是计算 \(\overline{err}(f(x),y,\overline{y})\) 时,我们需要知道所有满足 \( 1-f_y(x)+f_i(x) > 0 \) 的标签,因为:
- 计算 \(L(rank_y^1(f(x))\) 要用到(记得那个求和式子吗)
- 采样的第二步要用到(因为要从这些标签里采样)
论文中第 最聪明的地方 来了,作者提出了一个近似 \(\overline{err}(f(x),y,\overline{y})\) 的方法,解决以上两个问题:
在第二步的采样中,不再从满足 \( 1-f_y(x)+f_i(x) > 0 \) 的标签里采样,而是从 除去 \(y\) 的所有 标签里进行采样,如果采样到的标签 i 不满足 \( 1-f_y(x)+f_i(x) > 0 \),就把它放回,再次采样,直到找到满足条件的标签为止。
表面上,这解决了第二次采样的问题,这种有放回采样的效果,等价于原来的采样,而且不需要事先算出所有满足条件的标签。
但实际上,这也解决了第一个问题。假设一共有 \(k\) 个标签满足 \( 1-f_y(x)+f_i(x) > 0 \),那么,从所有标签中采样到这种标签的概率就是 \(P=\frac{k}{N-1}\),由于这种有放回采样满足 几何分布 (还记得大学概率课吗?一直投骰子,直到遇到6),所以期望的采样次数为:
\[ E[采样次数] = \frac{N-1}{k} \]
我们可以用实际的采样次数近似期望的采样次数,所以我们可以近似得到 \(k\) 的值为 \( \frac{N-1}{采样次数} \),于是可以算出 \(L(rank_y^1(f(x))\) 的近似值。
其它讨论
此外,论文还对 \(W\) 和 \(V\) 每一列的大小做了约束:
\[ ||W||_2 <= C,||V||_2 <= C \]
在优化时,如果某一列超过了 C,就将该列的值等比例缩小一下。
如果理解了后续的采样步骤,就会理解对损失函数的近似步骤:
之所以将 0/1 loss 近似为 hinge loss,是为了让损失函数连续,之所以用 \(rank_y^1(f(x),y) \) 替换 \(rank_y(f(x),y) \) ,是为了在第二步采样时去掉分母
在训练过程的每一步,都仅涉及一个训练数据 \((x,y)\),以及后续的几条采样数据,这种 online learning 的学习方法适用于海量数据集。
实际应用中,每个对象会有 多个标签,在训练时,可以针对每个标签单独跑一次采样,
此外,我还有一个想法,模型中的输入 feature 已经是计算好了的,我们也可以把原始的数据直接放入模型,例如,利用 NN 自动学习出特征,实现 end-to-end 的打标签架构。
算法名字很像"芥末",所以文章的开头我放了芥末。